前言
本库提供相机校准脚本,原理是通过使用摄像头在线抓取多个校准图案,然后求出相机内参。
环境
系统环境
Distributor ID: Ubuntu
Description: Ubuntu 18.04.4 LTS
Release: 18.04
Codename: bionic
Linux version : 5.3.0-46-generic ( buildd@lcy01-amd64-013 )
Gcc version: 7.5.0 ( Ubuntu 7.5.0-3ubuntu1~18.04 )
软件信息
version :
None
正文
理论原理
什么是相机内参?
相机内参既是相机模型参数,每个相机的内参都不一致,可以从出厂设置时候获取和自行标定计算出来。
通常认为相机的内参在出厂之后是固定的,不会在使用的过程中发生变化。
内参数 = 映射模型+畸变模型
映射模型:相机将三维世界中的坐标点(单位米)映射到二维图像平面(单位像素)的过程,针孔模型是其中之一
畸变模型:由于相机镜头上的透镜存在,使得光线投影到平面的过程。
这里只讨论针孔相机模型,不涉及外参
映射模型
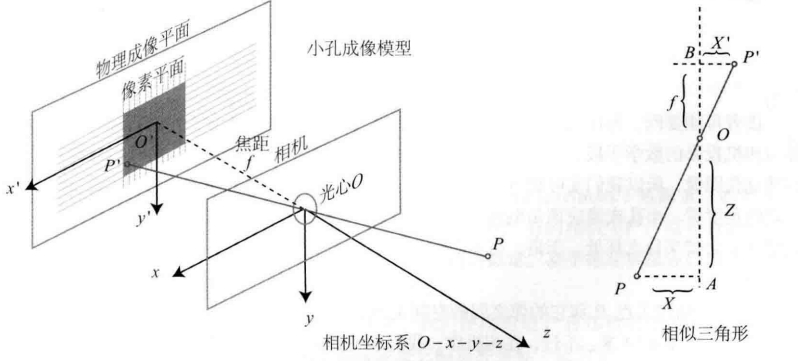
引用**像素坐标系 **$o-u-v$,像素坐标系与成像平面之间,相差了一个缩放和一个原点平移。
根据三角形相似和坐标系转换(三维和像素)
得到:
$Z\left(\begin{array}{l}
u
v
1
\end{array}\right)=\left(\begin{array}{ccc}
f_{x} & 0 & c_{x}
0 & f_{y} & c_{y}
0 & 0 & 1
\end{array}\right)\left(\begin{array}{c}
X
Y
Z
\end{array}\right) \stackrel{\text { def }}{=} \boldsymbol{K} \boldsymbol{P}$
其中,$f_{x}, f_{y} $和$ c_{x}, c_{y}$的单位为像素。$f_x = \alpha f, f_y= \beta f$,$f$为焦距
P点和$P^{\prime}$的关系:设像素坐标在$u$轴缩放了$\alpha$倍,在$v$轴上缩放了$\beta$倍,同时原点平移了$\left[c_{x}, c_{y}\right]^{\mathrm{T}}$
$ K =\left(\begin{array}{ccc}
f_{x} & 0 & c_{x}
0 & f_{y} & c_{y}
0 & 0 & 1
\end{array}\right)$,从该公式看,只与焦距有关。
矩阵K就是相机的内参数,通常认为相机的内参在出厂之后是固定的,不会在使用的过程中发生变化。
畸变模型
畸变分成两种:
-
径向畸变:由于透镜形状引起的,径(光线往中心走)
桶形和枕形两种畸变中,穿过图像中心和光轴有交点的直线还能保持形状不变。
- 桶形畸变,图像放大率随着与光轴之间的距离增加而减少。
- 枕形畸变,图像放大率随着与光轴之间的距离减少而增加。
-
切向畸变:由于组装过程中不能是透镜和成像面严格平行引发的。
两种畸变都有解决方案:去畸变处理(Undistort)畸变校正处理。
总结:
相机矩阵:包括焦距(fx,fy),光学中心(Cx,Cy),完全取决于相机本身,是相机的固有属性,只需要计算一次,可用矩阵表示如下:[fx, 0, Cx; 0, fy, Cy; 0,0,1];
畸变系数:畸变数学模型的5个参数 D = (k1,k2, P1, P2, k3);
相机内参:相机矩阵和畸变系数统称为相机内参,在不考虑畸变的时候,相机矩阵也会被称为相机内参;
单目相机的成像过程:
- 世界坐标系下有一个固定的点P,世界坐标为$P_W$
- 由于相机在运动,相机的运动由$R,t$描述,P的相机坐标为$\tilde{\boldsymbol{P}}_{\mathrm{c}} = RP_W + t$。
- 这时的$\tilde{\boldsymbol{P}}{\mathrm{c}}$的分量为$X,Y,Z$,把它们投影到归一化平面$Z=1$,得到P的归一化坐标:$\boldsymbol{P}{\mathrm{c}}=[X / Z, Y / Z, 1]^{\mathrm{T}}$,注意,Z可能小于1,说明该点位于归一化平面后面,它可能不会在相机平面上成像,实践中要检查一次。
- 有畸变时,根据畸变参数计算$P_c$发生畸变后的坐标。
- P的归一化坐标经过内参后,对应到它的像素坐标:$\boldsymbol{P}{u v}=\boldsymbol{K} \boldsymbol{P}{\mathrm{c}}$
综上所述,一共有四种坐标: 世界坐标(三维世界),相机坐标(相机位置),归一化坐标(成像平面),像素坐标(图片)
最后用一幅图来总结从世界坐标系到像素坐标系(不考虑畸变)的转换关系:
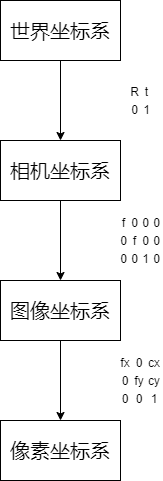
代码理解
-
findChessboardCorners() 棋盘格角点检测
cv.findChessboardCorners(image, patternSize[, corners[, flags]] ) -> retval,corners 参数: image 输入的棋盘格图像(可以是8位单通道或三通道图像); patternSize 棋盘格内部的角点的行列数(注意:不是棋盘格的行列数,如棋盘格的行列数分别为4、8,而内部角点的行列数分别是3、7,因此这里应该指定为cv::Size(3, 7)); corners 检测到的棋盘格角点,类型为std::vectorcv::Point2f。 flags 用于指定在检测棋盘格角点的过程中所应用的一种或多种过滤方法,可以使用下面的一种或多种,如果都是用则使用OR: cv::CALIB_CB_ADAPTIVE_THRESH:使用自适应阈值将图像转化成二值图像 cv::CALIB_CB_NORMALIZE_IMAGE:归一化图像灰度系数(用直方图均衡化或者自适应阈值) cv::CALIB_CB_FILTER_QUADS:在轮廓提取阶段,使用附加条件排除错误的假设 cv::CALIB_CV_FAST_CHECK:快速检测
-
cornerSubPix() 亚像素检测
cv.cornerSubPix(image, corners, winSize, zeroZone, criteria ) -> corners 参数: image 源图像 corners 提供角点的初始坐标,返回更加精确的点 winSize 搜索窗口的一般尺寸,如果winSize=Size(5,5),则search windows为1111 zeroZone 死区的一般尺寸,用来避免自相关矩阵的奇点,(-1,-1)表示没有死区 criteria 控制迭代次数和精度 -
drawChessboardCorners() 棋盘格角点绘制
cv.drawChessboardCorners(image, patternSize, corners, patternWasFound) -> image 参数: image 8-bit,三通道图像 patternSize 每一行每一列的角 corners 已经检测到的角 patternWasFound findChessboardCorners的返回值 -
calibrateCamera() 求解摄像头的内在参数和外在参数
#include <opencv2/calib3d.hpp> python: cv.calibrateCamera( objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]] -> retval, cameraMatrix, distCoeffs, rvecs, tvecs 参数: objectPoints 世界坐标,用vector,输入x,y坐标,z坐标为0 imagePoints 图像坐标,vector imageSize,图像的大小用于初始化标定摄像机的image的size cameraMatrix,内参数矩阵 distCoeffs,畸变矩阵 rvecs,位移向量 tvecs,旋转向量 flags,可以组合: CV_CALIB_USE_INTRINSIC_GUESS:使用该参数时,将包含有效的fx,fy,cx,cy的估计值的内参矩阵cameraMatrix,作为初始值输入,然后函数对其做进一步优化。如果不使用这个参数,用图像的中心点初始化光轴点坐标(cx, cy),使用最小二乘估算出fx,fy(这种求法好像和张正友的论文不一样,不知道为何要这样处理)。注意,如果已知内部参数(内参矩阵和畸变系数),就不需要使用这个函数来估计外参,可以使用solvepnp()函数计算外参数矩阵。 CV_CALIB_FIX_PRINCIPAL_POINT:在进行优化时会固定光轴点,光轴点将保持为图像的中心点。当CV_CALIB_USE_INTRINSIC_GUESS参数被设置,保持为输入的值。 CV_CALIB_FIX_ASPECT_RATIO:固定fx/fy的比值,只将fy作为可变量,进行优化计算。当CV_CALIB_USE_INTRINSIC_GUESS没有被设置,fx和fy的实际输入值将会被忽略,只有fx/fy的比值被计算和使用。 CV_CALIB_ZERO_TANGENT_DIST:切向畸变系数(P1,P2)被设置为零并保持为零。 CV_CALIB_FIX_K1,…,CV_CALIB_FIX_K6:对应的径向畸变系数在优化中保持不变。如果设置了CV_CALIB_USE_INTRINSIC_GUESS参数,就从提供的畸变系数矩阵中得到。否则,设置为0。 CV_CALIB_RATIONAL_MODEL(理想模型):启用畸变k4,k5,k6三个畸变参数。使标定函数使用有理模型,返回8个系数。如果没有设置,则只计算其它5个畸变参数。 CALIB_THIN_PRISM_MODEL (薄棱镜畸变模型):启用畸变系数S1、S2、S3和S4。使标定函数使用薄棱柱模型并返回12个系数。如果不设置标志,则函数计算并返回只有5个失真系数。 CALIB_FIX_S1_S2_S3_S4 :优化过程中不改变薄棱镜畸变系数S1、S2、S3、S4。如果cv_calib_use_intrinsic_guess设置,使用提供的畸变系数矩阵中的值。否则,设置为0。 CALIB_TILTED_MODEL (倾斜模型):启用畸变系数tauX and tauY。标定函数使用倾斜传感器模型并返回14个系数。如果不设置标志,则函数计算并返回只有5个失真系数。 CALIB_FIX_TAUX_TAUY :在优化过程中,倾斜传感器模型的系数不被改变。如果cv_calib_use_intrinsic_guess设置,从提供的畸变系数矩阵中得到。否则,设置为0。
实操
步骤:
- 打印 pattern.png 并将其粘贴到实心板上
- 固定相机镜头变焦,校准值随镜头变焦变化而变化
- 录制视频,图案在相机前移动
- 图案大部分时间应该是完全可见的
- 尝试移动图案以覆盖相机视图的所有部分,注意角落
- 视频长度应为 1 或 2 分钟
- 运行calibration.py从视频中提取棋盘图案角并执行相机校准
$ mkdir out
$ calibrate.py example_input/chessboard.avi calibration.yaml --debug-dir out
有时候无法检测到棋盘格角点,导致无法计算摄像头的内参数
使用camera-calibration.py 得到某摄像头的内参:
rms, camera_matrix, dist_coefs, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, (w, h), None, None)
return {'RMS': rms, 'cam_matrix': camera_matrix,
'distortion coef': dist_coefs}
RMS: 0.7904033508165567
cam_matrix: [[339.04918574367036, 0.0, 324.4578306708091], [0.0, 354.55587891010885, 249.2879173320891], [0.0, 0.0, 1.0]]
distortion coef: [[-0.2637199595877457, 0.04944373758433949, 0.0021764838280600063, -0.0007236132861065995, 0.0029699959816359145]]
由相机矩阵和畸变系数得
cameraMatrix = [ [fx, 0, Cx]; [0, fy,Cy]; [0,0,1]]
DistCoeffs = [K1, K2, P1, P2, K3]
得到
# Camera calibration and distortion parameters (OpenCV) , 一般切成6个小数点
Camera.fx: 339.049185
Camera.fy: 354.555878
Camera.cx: 324.457830
Camera.cy: 249.287917
Camera.k1: -0.263719
Camera.k2: 0.049443
Camera.p1: 0.002176
Camera.p2: -0.000723
Camera.k3: 0.002969